GPS和LPR轨迹数据的纠偏

发表于 | 阅读次数：

GPS漂移处理

GPS 轨迹点的漂移，最常见于当车辆进入隧道等 GPS 信号弱的区间时，本该位于区间内的 GPS 定位点却停留在入口处，而等到车辆驶出区间后，GPS 点又瞬移到出口处。这种情况下，我们利用 GPS 数据计算车速时会出现区间内速度为 0，出口处又严重超速的现象，且车辆定位不准确同样影响会空间分析的结果，因此，需要进行修正。

对于这类偏移，很直接的思路是将车辆看作以匀速通过区间，把 GPS 定位点按等间隔还原到轨迹上。首先需要找到 GPS 发生漂移的位置（出口处的第一个数据点），从该点向前倒推，将停滞在同一位置不动的点找出来。以它们与出口的距离作为待分配位移，以这些点的总间隔时间为待分配时间，求出通过区间的平均速度，最后根据时间戳为每个停滞点分配对应的位移。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def tunnel_gps_rectification(points, cal_distance, t):
    geom = LineString(points)  # 原始轨迹点序列
    mileage = [cal_distance(points[i-1], points[i]) for i in range(1, len(points))]  # cal_distance为两点间距离函数
    mileage.insert(0, 0)
    mileage = np.array(mileage).cumsum()
    
    speed = np.diff(mileage) / np.diff(t)
    overspeed_idxs = np.where(speed > 41.67)[0]  # 超速筛选阈值，这里用150km/h
    for idx in overspeed_idxs:
        start_mileage = mileage[idx]
        for i in range(idx, -1, -1):
            if start_mileage - mileage[i] < 1:  # 位移小于1m的点认为停滞
                trace = i
            else:
                break

        mileage_to_allocate = mileage[idx+1] - mileage[trace]
        time_to_allocate = t[idx+1] - t[trace]
        avg_speed = mileage_to_allocate/time_to_allocate

        for i in range(trace+1, idx+1):
            mileage[i] = mileage[i-1] + avg_speed * (t[i]-t[i-1])
            
    new_points = [geom.interpolate(loc, normalized=False).coords[0] for loc in mileage]  
    return new_points

函数的入参points可以直接使用原始 GPS 轨迹序列，但在GPS定位精度不足或采样频率太低的情况下，有条件应考虑先对轨迹数据进行地图匹配，如使用基于隐马尔可夫模型的leuvenmapmatching等算法以获取精确的轨迹点位置和位移。

LPR与GPS的轨迹融合

LPR (License Plate Recognition) 数据样本量大但采样频率低，而 GPS 数据采样频率高但样本量少。因此我的一个 idea 是尝试融合两类数据，并用 LPR 数据还原出 GPS 轨迹的特征。但实际中将同一辆车的 GPS 与 LPR 数据按照时间戳进行直接拼接，往往会产生很多问题，比如在轨迹中出现异常的折返，如下图：

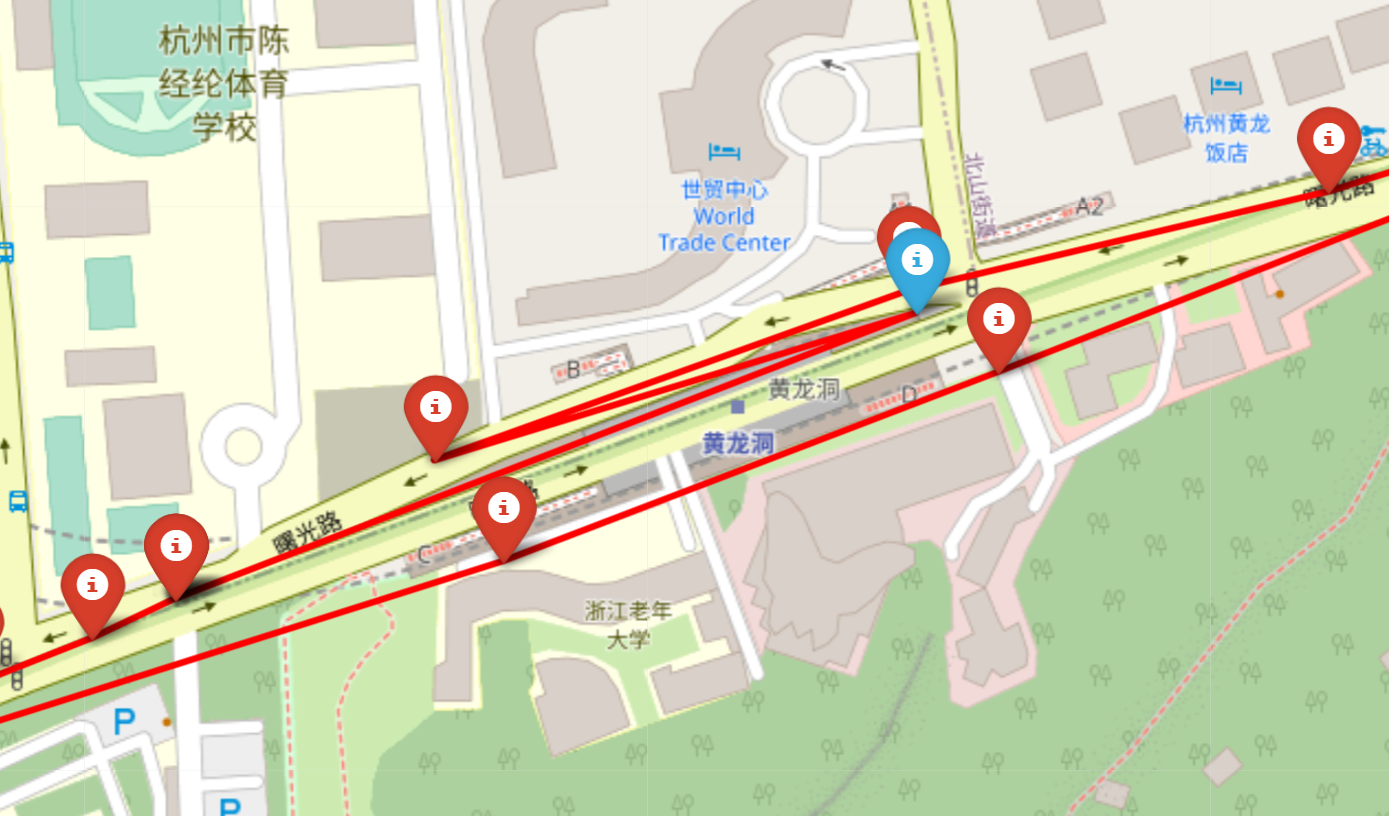
同样会导致速度计算的异常。有多种原因可能产生这种折返现象：
- LPR 系统与 GPS 系统的时钟不同步
- LPR 过车数据实际上记录的是车辆通过停车线的时间，而停车线位置与设备位置不完全相同
- 同上述原因，可能有车辆在路口停车时已经超出停车线，产生错误记录

由于 LPR 设备位置是稳定的，不存在像 GPS 的偏移情况，因此解决这个问题可以通过固定 LPR 记录的位置，而调整对应的时间戳，使得其与 GPS 数据更好地融合。算法的思路是以每条 LPR 记录的原始时间戳为中心，定义一个时间窗，并在窗内前后移动时间戳。最终，找到某个时间戳使得 LPR 数据点与其前后两个 GPS 数据点形成的折线距离最小（轨迹最顺滑），且 LPR 点到前后 GPS 点的两段平均速度与两个 GPS 点间的平均速度最为接近。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
def adjust_lpr_timestamp(lpr_timestamp, lpr_idx, gps_t, gps_point, lpr_point, cal_distance, tw=30):
    results = []
    for moving_timestamp in range(lpr_timestamp-tw, lpr_timestamp+tw+1):
        indexs = np.where(moving_timestamp <= gps_t)[0]
        if len(indexs) == 0:  # LPR点是轨迹点序列的最后一个
            right_idx = len(gps_t) - 1
            left_idx = right_idx - 1
            gps_dist = cal_distance(gps_point[left_idx], gps_point[right_idx])
            lpr_dist = cal_distance(gps_point[right_idx], lpr_point[lpr_idx])
            mileage = gps_dist + lpr_dist
            if (moving_timestamp - gps_t[right_idx]) == 0:  # LPR与GPS时间戳重叠
                lpr_speed_1, lpr_speed_2 = 9999, 9999
            else:
                lpr_speed_1 = lpr_dist / (moving_timestamp - gps_t[right_idx])
                lpr_speed_2 = lpr_speed_1
        else:
            right_idx = indexs[0]
            if right_idx == 0:  # LPR点是轨迹点序列的第一个
                left_idx = 0
                right_idx = 1
                gps_dist = cal_distance(gps_point[left_idx], gps_point[right_idx])
                lpr_dist = cal_distance(lpr_point[lpr_idx], gps_point[left_idx])
                mileage = lpr_dist + gps_dist
                if (gps_t[left_idx] - moving_timestamp) == 0:
                    lpr_speed_1, lpr_speed_2 = 9999, 9999
                else:
                    lpr_speed_1 = lpr_dist / (gps_t[left_idx] - moving_timestamp)
                    lpr_speed_2 = lpr_speed_1
            else:
                left_idx = right_idx - 1
                gps_dist = cal_distance(gps_point[left_idx], gps_point[right_idx])
                lpr_dist_1 = cal_distance(gps_point[left_idx], lpr_point[lpr_idx])
                lpr_dist_2 = cal_distance(lpr_point[lpr_idx], gps_point[right_idx])
                mileage = lpr_dist_1 + lpr_dist_2
                if (moving_timestamp - gps_t[left_idx] == 0) or (gps_t[right_idx] - moving_timestamp == 0):
                    lpr_speed_1, lpr_speed_2 = 9999, 9999
                else:
                    lpr_speed_1 = lpr_dist_1 / (moving_timestamp - gps_t[left_idx])
                    lpr_speed_2 = lpr_dist_2 / (gps_t[right_idx] - moving_timestamp)
        gps_speed = gps_dist / (gps_t[right_idx] - gps_t[left_idx])
        speed_diff = abs(gps_speed - lpr_speed_1) + abs(gps_speed - lpr_speed_2)  # GPS与LPR速度差
        results.append([mileage, speed_diff])
    results = np.array(results) 
    adjust_idx = np.lexsort((results[:,0], results[:,1]))[0]  # 按最小位移和最小速度差排序
    return lpr_timestamp - tw + adjust_idx