最近在尝试做时间序列数据的缺失值填补,由于数据的缺失率很高(80% 以上)且这一部分预计是研究的重点和亮点,想到了用深度学习方法来做填补。在网上搜索资料发现,现有的模型很多都使用了 GAN 框架,比如 GAIN (ICML 2018),E2GAN (NIPS 2018, IJCAI 2019),这些都是发表在计算机顶会上的成果。后者参考资料比较多,我打算用这个框架进行尝试,这也是我第一次正儿八经地做模型复现。幸运的是,我找到了论文一作的GitHub 项目,不至于从零开始。但这个项目基于 Python 2.7 和 Tensorflow 1.7,有些陈旧了。我参考源码和论文,按个人理解用 Python 3和Pytorch 复现了这一模型结构。
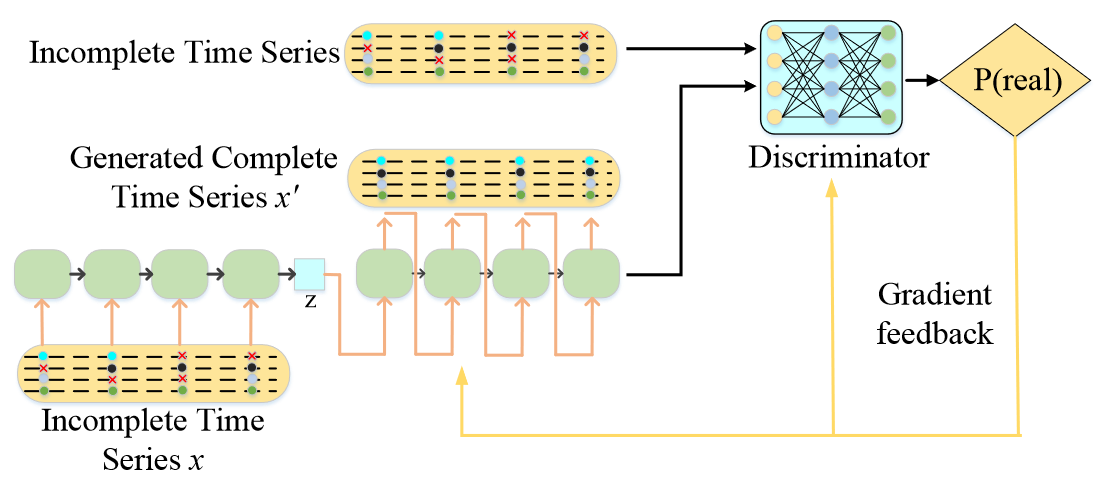
E2GAN总体框架
模型结构
和大部分 GAN 一样,E2GAN 也是由一个生成器(Generator)和一个判别器(Discriminator)组成。其中,生成器的部分是一个自动编码器(Auto-Encoder)结构,原始的不完整时间序列输入 \(x\) 会被加上一个随机噪声 \(\eta\),送入 RNN 网络进行编码,压缩为一个一维向量 \(z\),再经过 RNN 解码,逐个时间步地生成完整序列 \(x^{'}\)。判别器的结构相对简单,对输入的数据用同样的 RNN 结构提取特征,最后用全连接层映射到一个输出。
损失函数
E2GAN的损失函数参考了Wasserstein GAN(WGAN),但做了一些修改。具体来说,文章定义了以下几个损失:
遮盖重建损失(Masked Reconstruction Loss) \(L_r(z)=\Vert X \odot M - G(z) \odot M\Vert_2\)
判别损失(Discriminative Loss) \(L_d(z) = -D(G(z))\)
插补损失(Imputation Loss) \(L_{imputation}(z) = L_r(z) + \lambda L_d(z)\)
其中,插补损失即为生成器损失,相比 WGAN 多加了一项遮盖重建损失,并使用 \(\lambda\) 调节大小。整个模型需要优化的判别器与生成器损失为:
\[L_G = L_r(z) + \lambda L_d(z)\] \[L_D = D(x) - L_G\]
GRUI cell
可以看出,E2GAN 的生成器和判别器里都使用了同一种 RNN 网络,是整个模型的核心。这里使用的 RNN 是作者在 NIPS 的文章中提出的 GRUI(Gated Recurrent Unit for data Imputation),一种 GRU 的变体。
GRUI 的最大改变是引入了一个 0-1 之间的时间衰减向量 \(\beta\) 来控制历史时间步的影响。\(\beta\) 的表达式为 \(\beta_{t_i}=e^{-\max (0, W_\beta \delta_{t_i}+b_\beta)}\),这里的 \(\delta\) 是序列 \(x\) 对应时间步的滞后时长(time lag)。
1 | beta = self.beta_fc(delta) # Linear layer |
加入 \(\beta\) 后,GRUI 的计算过程与 GRU 大同小异: \[ h^{'}_{t_{i-1}} = \beta_{t_i} \odot h_{t_{i-1}} \\ \mu_{t_i} = \sigma(W_\mu [h^{'}_{t_{i-1}},x_{t_i}]+b_\mu) \\ r_{t_i} = \sigma(W_r [h^{'}_{t_{i-1}},x_{t_i}]+b_r) \\ \tilde h_{t_i} = \tanh(W_{\tilde h} [r_{t_i} \odot h^{'}_{t_{i-1}},x_{t_i}]+b_{\tilde h}) \\ h_{t_i} = (1 - \mu_{t_i}) \odot h^{'}_{t_{i-1}} + \mu_{t_i} \odot \tilde h_{t_i} \]
为了方便,我与作者源码保持一致,把 \(\beta\) 和每个时间步的输入 concat
在了一起,所以多了一个拆分的操作。此外,由于输入的序列不定长,传入的
batch size
是不固定的,而隐状态的大小固定,因此将已经不需要更新的隐状态(已经超过实际序列长度)拆出来,最后再合并,代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class GRUI(nn.Module):
def __init__(self, input_dim, hidden_dim):
super(GRUI, self).__init__()
lb, ub = -np.sqrt(1 / hidden_dim), np.sqrt(1 / hidden_dim)
self.hidden_dim = hidden_dim
self.w_x = nn.ParameterList([self.__init(lb, ub, input_dim, hidden_dim) for _ in range(3)])
self.w_h = nn.ParameterList([self.__init(lb, ub, hidden_dim, hidden_dim) for _ in range(3)])
self.b = nn.ParameterList([self.__init(lb, ub, hidden_dim) for _ in range(3)])
def __init(low, upper, dim1, dim2=None):
if dim2 is None:
return nn.Parameter(torch.rand(dim1) * (upper - low) + low)
else:
return nn.Parameter(torch.rand(dim1, dim2) * (upper - low) + low)
def forward(self, x, hid):
actual_size, total_len = x.shape
beta = x[:, total_len - self.hidden_dim:]
x = x[:, :total_len - self.hidden_dim]
inactive_hid = hid[actual_size:]
hid = hid[:actual_size]
hid = torch.mul(beta, hid)
mu = torch.sigmoid(torch.mm(x, self.w_x[0]) + torch.mm(hid, self.w_h[0]) + self.b[0])
r = torch.sigmoid(torch.mm(x, self.w_x[1]) + torch.mm(hid, self.w_h[1]) + self.b[1])
h_tilda = torch.tanh(torch.mm(x, self.w_x[2]) + torch.mm(torch.mul(r, hid), self.w_h[2]) + self.b[2])
next_hid = torch.mul((1 - mu), hid) + torch.mul(mu, h_tilda)
next_hid = torch.cat([next_hid, inactive_hid], 0)
return next_hid
Encoder
Encoder 的作用是在生成器中把原始输入压缩为向量 \(z\),具体步骤包括添加噪声 \(\eta\)、计算 \(\beta\)、输入 GRUI
网络,将最后的隐状态通过线性层映射到 \(z\)。pack_padded_sequence操作也写在了这里来处理不定长序列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40class Encoder(nn.Module):
def __init__(self, config):
super(Encoder, self).__init__()
self.hidden_dim = config.g_hidden_dim
self.config = config
self.beta_fc = nn.Linear(config.input_dim, config.g_hidden_dim)
self.output_fc = nn.Linear(config.g_hidden_dim, config.z_dim)
self.grui_cell = GRUI(config.input_dim, config.g_hidden_dim)
self.dropout = nn.Dropout(config.dropout_prob)
def forward(self, x, delta, length):
batch_size, seq_len, input_dim = x.shape
eta = torch.normal(mean=0.0, std=0.01, size=x.shape)
x = x + eta
x = x.reshape(-1, input_dim)
delta = delta.reshape(-1, input_dim) # -> batch_size*seq_len, input_dim
beta = self.beta_fc(delta)
beta_init = torch.zeros(delta.shape[0], self.hidden_dim).to(self.config.device)
beta = torch.exp(-torch.maximum(beta_init, beta))
x = torch.cat([x, beta], 1) # -> batch_size*seq_len, input_dim+hidden_dim
x_in = x.reshape(batch_size, seq_len, input_dim + self.hidden_dim)
# pack
packed = pack_padded_sequence(x_in, length, batch_first=True)
x_in = packed.data # total_size, input_dim+self.hidden_dim
sizes = packed.batch_sizes
hidden = torch.zeros(batch_size, self.hidden_dim).to(self.config.device)
start_idx = 0
for size in sizes:
x_step = x_in[start_idx: start_idx + size]
hidden = self.grui_cell(x_step, hidden)
start_idx += size
hidden = self.dropout(hidden)
z_output = self.output_fc(hidden) # batch_size, z_dim
return z_output, sizes
Generator
封装了 GRUI 和 Encoder 之后,生成器的结构就比较简单了。将输入压缩到
\(z\) 之后,输入另一个 GRUI
网络,从第一个时间步开始进行序列生成。需要注意的是这里 GRUI 使用的 \(\beta\) 与 Encoder 中不同,是通过完整数据的
\(\delta_{imputed}\)
计算而来的,即相邻元素的差等于时间戳间隔。 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67class Generator(nn.Module):
def __init__(self, config):
super(Generator, self).__init__()
self.hidden_dim = config.g_hidden_dim
self.config = config
self.z_fc = nn.Linear(config.z_dim, config.input_dim)
self.beta_fc = nn.Linear(config.input_dim, config.g_hidden_dim)
self.output_fc = nn.Linear(config.g_hidden_dim, config.input_dim)
self.series_to_z = Encoder(config)
self.grui_cell = GRUI(config.input_dim, config.g_hidden_dim)
self.dropout = nn.Dropout(config.dropout_prob)
self.bn = nn.BatchNorm1d(config.seq_len)
def forward(self, x, delta, imputed_delta, length):
batch_size, seq_len, input_dim = x.shape
z, sizes = self.series_to_z(x, delta, length) # batch_size, z_dim
x = self.z_fc(z)
x = x.reshape(-1, input_dim) # batch_size, input_dim
delta_zero = torch.zeros(batch_size, input_dim).to(self.config.device)
beta = self.beta_fc(delta_zero)
beta_init = torch.zeros(delta_zero.shape[0], self.hidden_dim).to(self.config.device)
beta = torch.exp(-torch.maximum(beta_init, beta)) # batch_size*seq_len, hidden_dim
x = torch.cat([x, beta], 1)
x_in = x.reshape(-1, input_dim + self.hidden_dim) # first step input
hidden = torch.zeros(batch_size, self.hidden_dim).to(self.config.device)
hidden = self.grui_cell(x_in, hidden)
hidden = self.dropout(hidden)
out_predict = self.output_fc(hidden)
out_predict = out_predict.reshape(-1, 1, input_dim) # -> batch_size, 1, hidden_dim
total_result = torch.mul(out_predict, 1.0)
for i in range(1, seq_len):
out_predict = out_predict.reshape(batch_size, input_dim)
if i < len(sizes):
actual_size = sizes[i]
delta_normal = imputed_delta[:actual_size, i:(i + 1), :].reshape(actual_size, input_dim)
beta = self.beta_fc(delta_normal)
beta_init = torch.zeros(delta_normal.shape[0], self.hidden_dim).to(self.config.device)
beta = torch.exp(-torch.maximum(beta_init, beta)) # actual_size*seq_len, hidden_dim
done_predict = out_predict[actual_size:]
out_predict = out_predict[:actual_size]
x = torch.cat([out_predict, beta], 1) # -> actual_size, input_dim+hidden_dim
x_in = x.reshape(-1, input_dim + self.hidden_dim) # -> actual_size, input_dim+hidden_dim
hidden = self.grui_cell(x_in, hidden)
hidden = hidden[:actual_size]
hidden = self.dropout(hidden)
out_predict = self.output_fc(hidden)
out_predict = torch.cat([out_predict, done_predict])
out_predict = out_predict.reshape(-1, 1, input_dim) # -> actual_size, 1, input_dim
total_result = torch.cat([total_result, out_predict], 1)
else:
pad = torch.zeros(batch_size, seq_len - len(sizes), input_dim).to(self.config.device)
total_result = torch.cat([total_result, pad], 1) # batch_size, seq_len, input_dim
break
if self.config.is_bn:
total_result = self.bn(total_result)
return total_result
Discriminator
判别器的结构比较简单,和 Encoder 类似,最后的线性层把输入序列映射到
batch size*1,由于采用了 WGAN loss,输出不需要加入 sigmoid 层。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36class Discriminator(nn.Module):
def __init__(self, config):
super(Discriminator, self).__init__()
self.hidden_dim = config.d_hidden_dim
self.config = config
self.beta_fc = nn.Linear(config.input_dim, config.d_hidden_dim)
self.output_fc = nn.Linear(config.d_hidden_dim, 1)
self.grui_cell = GRUI(config.input_dim, config.d_hidden_dim)
self.dropout = nn.Dropout(config.dropout_prob)
def forward(self, x, delta, length):
batch_size, seq_len, input_dim = x.shape
x = x.reshape(-1, input_dim) # batch_size*seq_len, input_dim
delta = delta.reshape(-1, input_dim) # batch_size*seq_len, input_dim
beta = self.beta_fc(delta)
beta_init = torch.zeros(delta.shape[0], self.hidden_dim).to(self.config.device)
beta = torch.exp(-torch.maximum(beta_init, beta)) # batch_size*seq_len, hidden_dim
x = torch.cat([x, beta], 1) # batch_size*seq_len, input_dim+hidden_dim
x_in = x.reshape(batch_size, seq_len, input_dim + self.hidden_dim)
packed = pack_padded_sequence(x_in, length, batch_first=True)
x_in = packed.data # total_size, input_dim+self.hidden_dim
sizes = packed.batch_sizes
hidden = torch.zeros(sizes[0], self.hidden_dim).to(self.config.device)
start_idx = 0
for size in sizes:
x_step = x_in[start_idx: start_idx + size]
hidden = self.grui_cell(x_step, hidden)
start_idx += size
hidden = self.dropout(hidden)
output = self.output_fc(hidden)
return output
总结
有作者源码的参考,复现整个模型结构并没有花费很多时间,反倒是后续调整输入、改 bug 浪费了大量时间。但尽管投入了很多精力去调整模型,E2GAN 在我的数据集上效果也并不好,甚至可以说非常差,生成器对原始输入的拟合效果不佳,遮盖重建损失下降缓慢。这其中可能有部分原因是我对 Tensorflow 不熟悉,在代码迁移的过程中有隐藏的 bug 没有发现,但整个模型也存在很多我觉得不合理的地方。例如,Encoder 只取了最后而不是每个时间步的隐状态为输出,一个一维的向量 \(z\) 可能很难提取出整个序列的特征;生成器逐个时间步生成序列,每个时间步过一次 GRUI 和同一个线性层,线性层的权重更新混乱,后续时间步也缺少 \(z\) 的信息等等。事实上,我在其他的模型中,用作者提出的 GRUI 代替原本的 GRU 和 LSTM 确实得到了更好的结果,因此,至少 Github 上这个版本的源码的模型结构可能存在问题。