好像有一阵子没更了,这两周导师临时派了很多事,加上快要结课和组会,端午三天的假期我肝了两天,也没有吃上粽子,总算是把所有的任务都做差不多了。这篇文献本来是准备在昨天的组会上分享的,没想到这周突然不开了,就在这里记录下来,也加深自己的印象~
文章概述
这篇文章是之前阿里的老师授课时提到的,正好组会要做论文分享,我就找来看了一下。文章标题直译过来是“人类移动性的普适访问规律”,发表在《Nature》正刊上,相当令人羡慕。人的移动性或者说人口流动在很多领域都是热门的研究方向。目前,在宏观层面描述移动性规律比较流行的模型是重力模型(gravity model)和辐射模型(radiation model),但这两个模型都只能获取 OD 之间的总流量,没有考虑到访问频率;同时,微观个体移动模型(比如EPR模型和容器模型)模拟的结果无法与宏观模型的结果很好的耦合。文章的主要贡献是发现了一个简单但有效的宏观移动性规律,成功地把访问频率纳入其中,并以 EPR 模型为基础,改进了微观移动模型,与提出的宏观模型衔接了起来。
文章使用手机信令数据,是移动性研究最常用的数据之一。每个研究区域被划分为边长 500m 或 1km 的正方网格,同时根据夜间停留位置确定手机用户的家庭位置,这些做法和以往的研究也是类似的。但是研究用的数据集规模很大,来自四个大洲的五个国家,可以说确实是具有普适性,这也是顶刊成果的特点。
人口流动的距离-频率规律
文章第一部分是介绍考虑频率的宏观移动性规律。网格 \(i\) 的每个访问用户都具有两个属性:访问半径 \(r\) 和访问频率 \(f\)。访问半径 \(r\) 即网格 \(i\) 到用户家庭位置的距离,实际上文中的距离 \(r\) 代表的是以网格 \(i\) 为圆心,半径 \(r\) 与 \(r+\delta r\) 之间的环形区域。将以频率 \(f\) 和距离 \(r\) 访问网格 \(i\) 的总访客流量 \(N_i(r,f)\) 除以环的面积 \(A(r)\) 得到流密度 \(\rho_i(r,f)\),文章称为“谱流”(spectral flow)。 在固定半径增加访问频率和固定访问频率增加半径两种情况下,谱流都逐渐下降(这点是显然的),有意思的是谱流随这两个变量变化的趋势高度一致,也就是变量是对称的。于是作者尝试构造新的变量 \(rf\),将谱流建模为关于 \(rf\) 单变量的函数,对各个国家的数据拟合的效果都非常好。
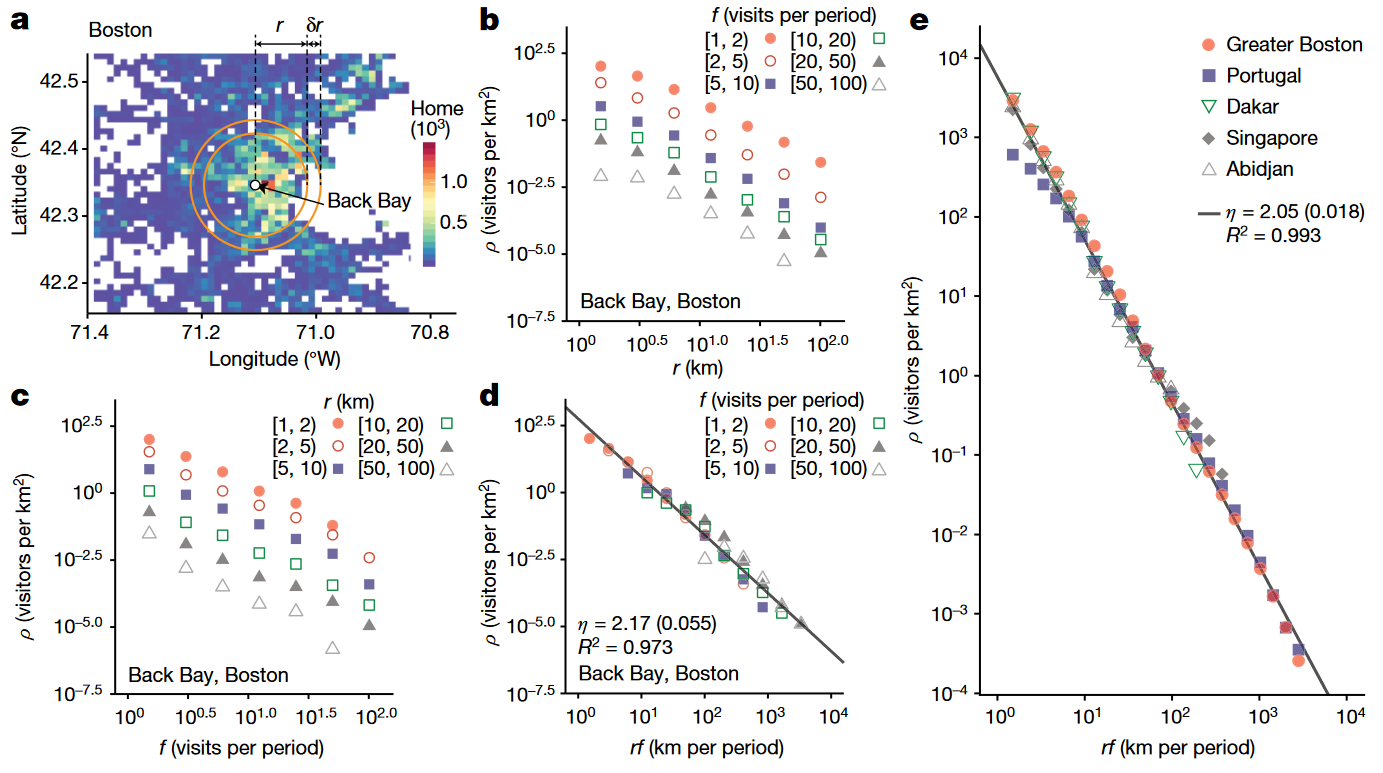
最后这一关系可以建模为: \[\rho_i(r,f) = \frac{\mu_i}{(rf)^\eta}\] 这个模型非常简单,分子的常数 \(\mu_i\) 决定了访问量的大小,因此反映的是网格 \(i\) 的吸引力。根据标定的结果,\(\eta\) 大概在2左右,即谱流与 \(rf\) 为反平方关系。后面的部分理解起来有些难度,作者进一步地用 \(v:=rf\) 表示模型中的单变量,可以发现 \(v\) 的量纲为距离/时间,与速度一致。把 \(v\) 定义为用户向目的地移动的有效速度(effective velocity),再乘以研究时长,就得到了用户移动的有效距离(effective distance)。
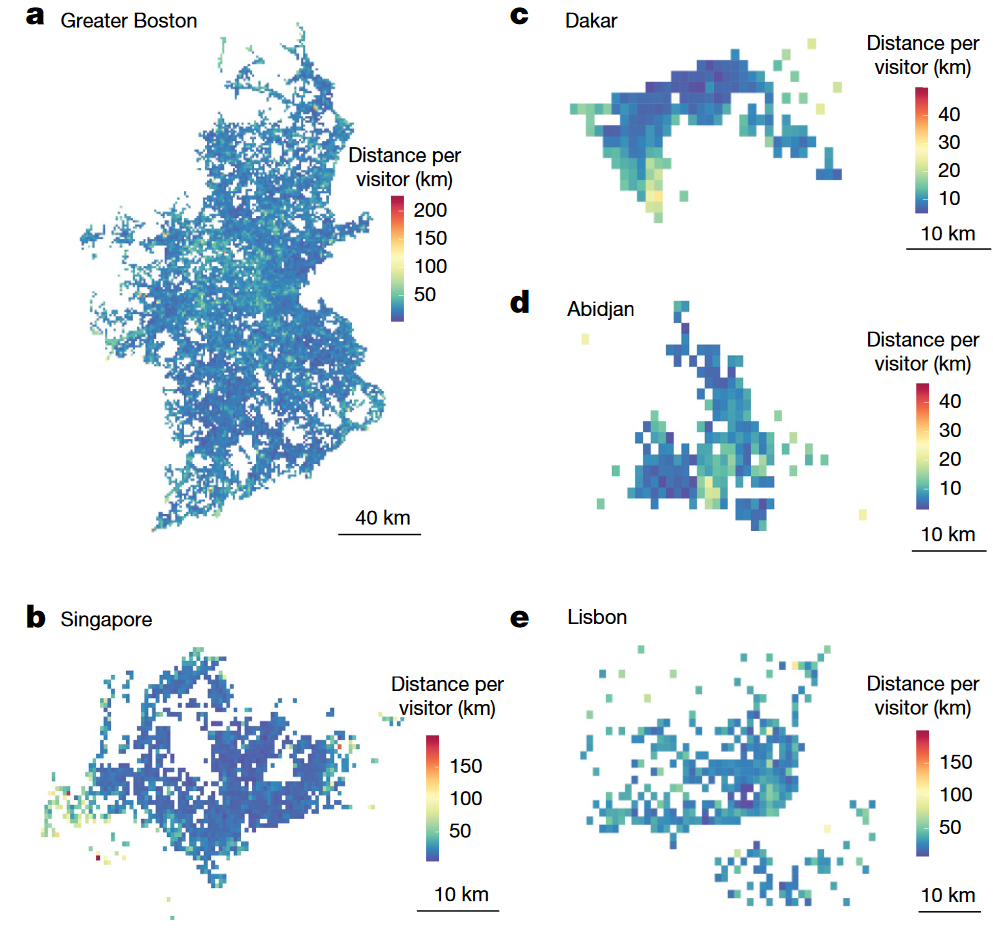
从有效距离出发,作者有了一个惊人发现:每个网格的访客的平均有效出行距离在整个城市范围内变化不大。这就是说,那些访客量很大的热门目的地(比如大型购物中心、医院)与路边的普通餐厅、商店比起来,并不会吸引用户更频繁地访问,也不会吸引更多远距离来访的用户,而只是单纯的近距离访客人数多而已。少数的例外是港口(对外交通枢纽)、旅游景点等具有不可替代性的地点。
地点吸引力的空间分布
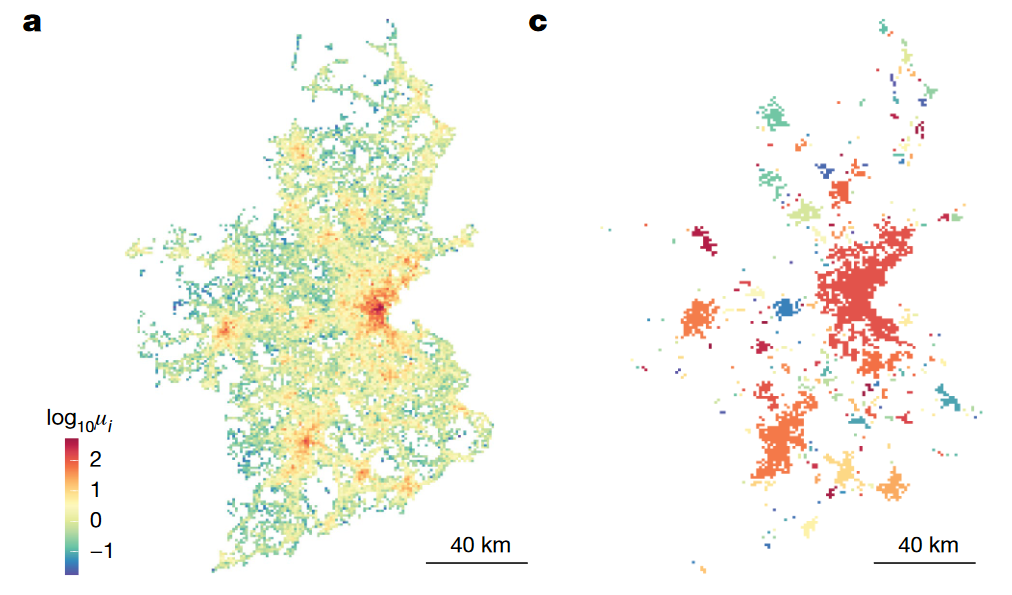
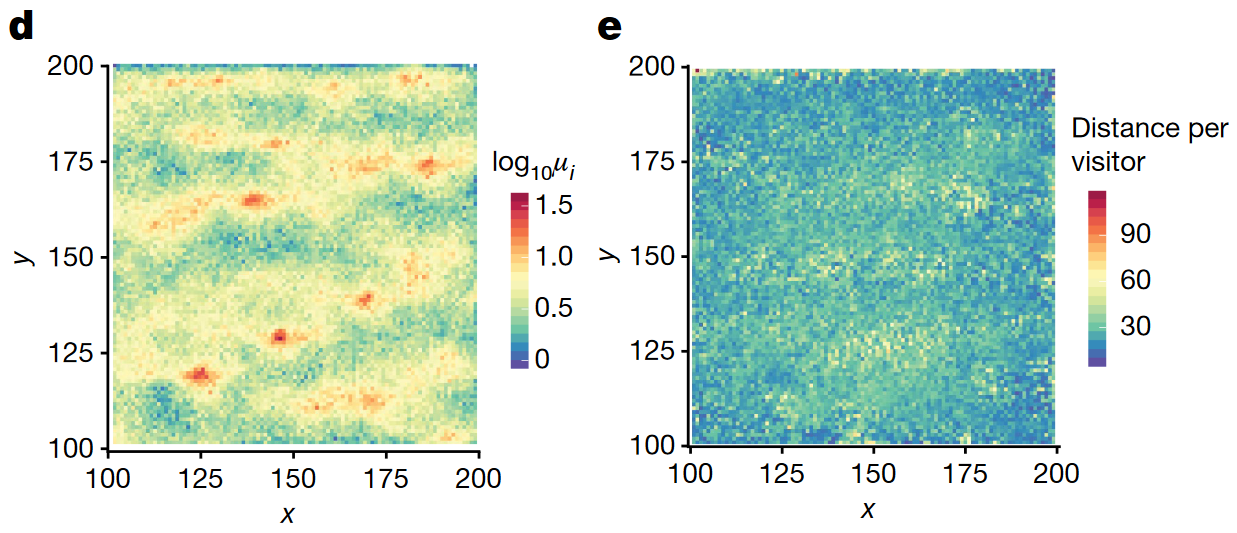
这一部分作者开始对网格的吸引力 \(\mu\) 进行分析。可视化的结果说明吸引力呈现簇状分布,较高吸引力的区域似乎被较低吸引力的区域围绕,这与以往很多城市结构的研究是相符的,比如中心地理论(Central Place Theory, CPT)。作者使用城市聚类算法(City Clustering Algorithm, CCA)进一步研究这些区域的大小。首先确定了一个吸引力阈值 \(\mu^*\),小于阈值的网格吸引力全部置为 0,之后对吸引力非0的网格开始聚类(这个算法的资料不多,感觉类似于一种自下而上的层次聚类)。聚类结果表明,簇的大小和它的大小对应的排名符合 Zipf 定律(也就是大小与排名成反比)。
改进的微观移动性模型
先简单介绍一下目前广泛使用的微观移动性模型——探索和偏好返回(Exploration and Preferential Return, EPR)模型。简单来说,在每个时间步,个体有两个行动选项:以概率 \(P_{new}\) 探索一个新地点;或者以互补概率 \(1-P_{new}\) 访问一个旧地点。其中新地点的探索是通过从一个长尾分布中取步长 \(\Delta r\),再从均匀分布中确定探索方向 \(\theta\) 实现的。
作者建立了一个规则的正方形区域,用 EPR 模型模拟个体行为,观察到群体表现出的宏观移动性特征同样与上文所述的谱流-距离频率规律相同(\(\eta\approx2\)),但吸引力的空间分布上,并没有呈现出簇状,而是高低网格均匀混合的。
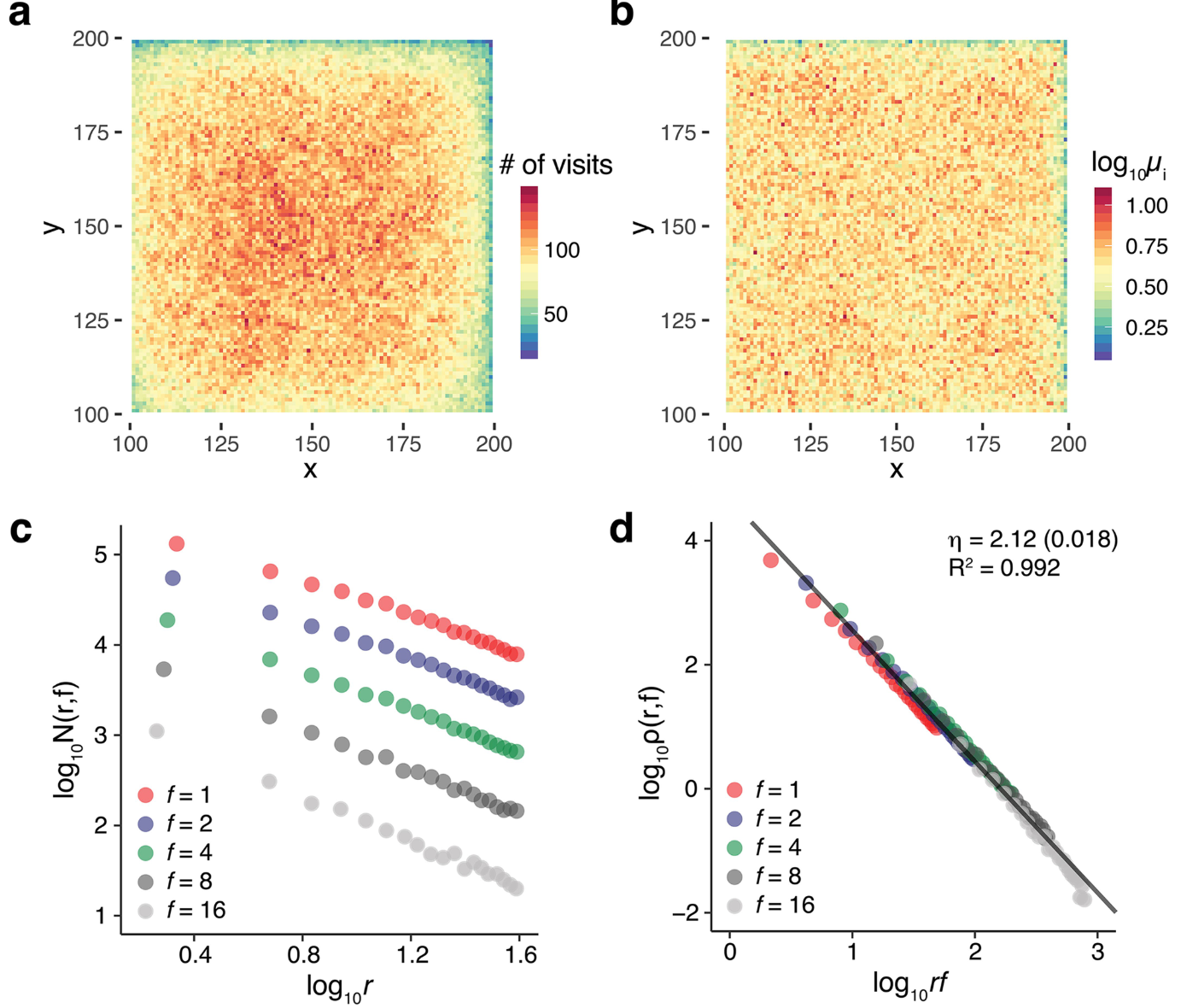
作者认为,出现该问题的原因在于个体选择访问地点时是独立的,并没有考虑到人类群体的相似行为。作者对 EPR 模型进行了简单修改,称为 PEPR(Preferential Exploration and Preferential Return)模型:探索新地点时,方向 \(\theta\) 并不是随机选择,而是偏向于高访问量的区域。PEPR 模型仿真的结果与实际数据的结果完全吻合,宏微观模型从而联系了起来。
运用规律进行OD预测
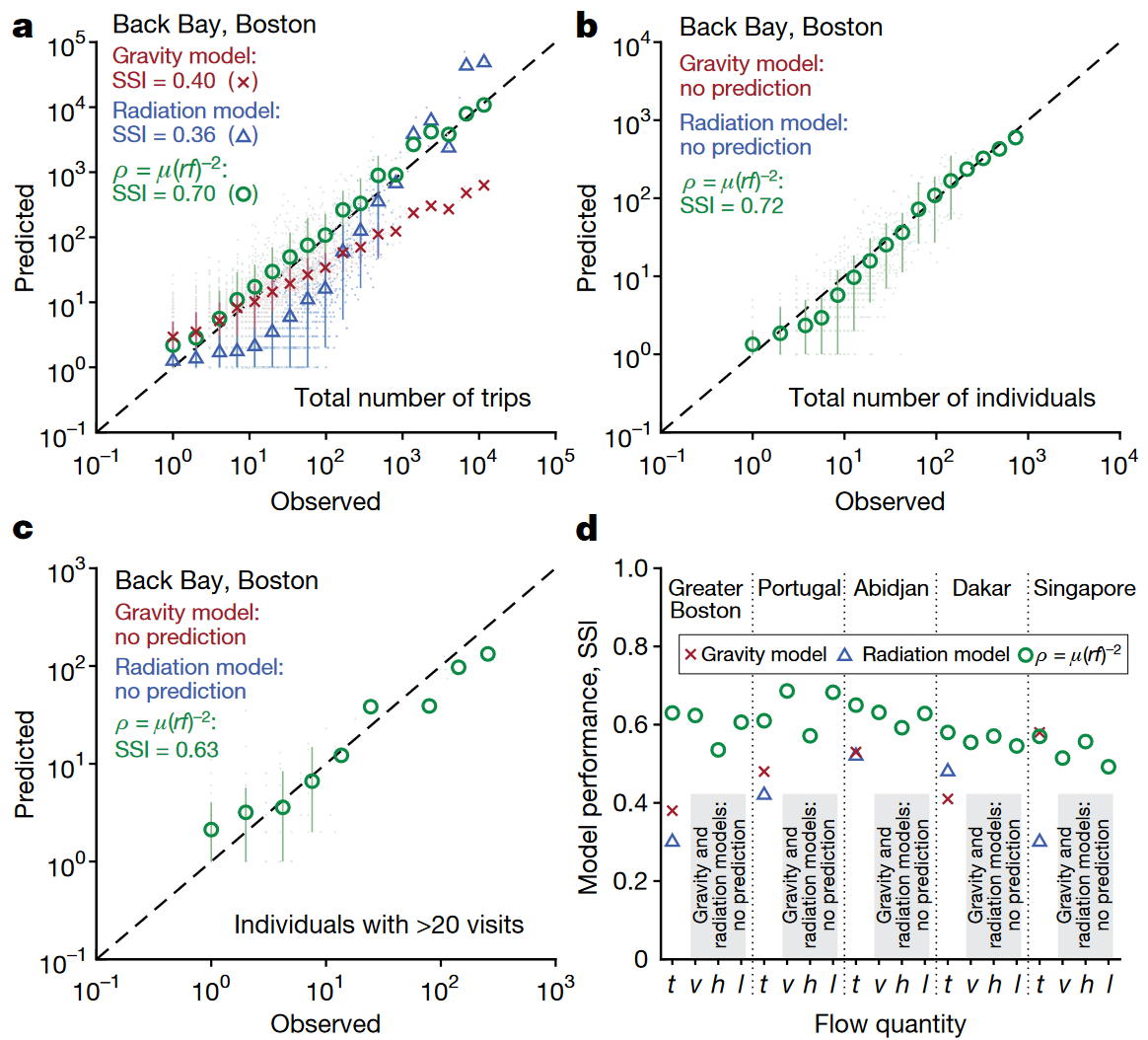
根据作者提出的移动性规律,理论上只需要知道某一地点的吸引力 \(\mu\),就可以计算以给定距离 \(r\) 和频率 \(f\) 访问该地点的流量。而吸引力 \(\mu\) 可以用多种特征进行计算,作者给出了一个通过人口密度估算的公式: \[\mu_i \approx \rho_{pop}(j)r_j^2f_{home}\] 其中 \(\rho_{pop}(j)\) 是网格 \(j\) 的人口密度,\(r_j\) 是到网格中心至边界的距离,\(f_{home}\approx 1 {day}^{-1}\) 代表用户返家的基本频率(假设每天至少回家一次)。利用谱流-距离频率规律的出行量预测精度显著高于重力模型和辐射模型的预测结果,且除了出行量之外,这一规律还可以对个体数量进行预测,这是重力模型和辐射模型所不具备的。
总结
这篇文章并没有用很多复杂深奥的方法,但是推导出的规律即简洁又有效,并且在多个国家的试验中都得到了验证,这是很难得的。文章的结论有符合认知和过往研究的,也有反常识但合理的亮点发现,所有的发现都能被恰当地解释。
移动性是交通研究中很重要的一块,比如出行行为分析和其他需要进行 OD 估计的地方,虽然和我目前的研究方向关系不大hhh,相信这篇文章的结果能派上用场。这篇文章给我的最大启发是 CCA 聚类时阈值 \(\mu^*\) 取值的思路——利用最大簇与所有簇的大小比来判断。之前在做关键通勤路径的研究时使用了 DBSCAN 聚类,超参数的取值非常难确定,最后靠人工调整完成。而当时想要的效果正是聚类出若干个明显的较大簇,与这篇文章的情景很相像。
我按照自己的理解总结了这篇文章的内容,在个别地方可能会有一些理解的偏差和错误。原文的一些细节内容,比如公式的推导,PERP 的原理等等我也没有放进来,有兴趣的读者可以参考原文和补充材料。
参考
Schläpfer, Markus, et al. "The universal visitation law of human mobility." Nature 593.7860 (2021): 522-527. https://doi.org/10.1038/s41586-021-03480-9